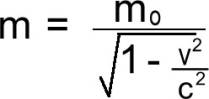
RELATIVISTIC MASS INCREASE

We have discussed the relative measurements of length and time in different reference frames (in time dialation and Length contraction). But there is one more thing that happens (out of the three we have discussed earlier)  when you travel at very high speeds.......Mass.

According to theory of relativity , moving objects have increased mass. You wont even believe how far you can push the scales to. I can become the heaviest person and enter Guinness Book of records....naah.its just too risky!

But the point here is that as an object approaches the speed of light, its mass increases infinitely. The mass of an object when traveling at high velocity is given by this formula :

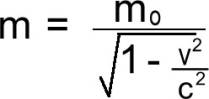
The Relativistic Mass Increase

One of the most sacred principles of physics is that of Momentum conservation. It means that the sum of momenta of two particles is the same before and after a collision between them. Now momentum is just the product of mass and velocity, and velocity is the quotient of distance and time [Remember The momentum equation: p=m*v and d=v*t].

Since both distance and time have different values when measured from different frames of reference [as discussed in length contraction and time dialation]. It is perhaps not too surprising that velocity demonstrates a relativistic effect. But if the value of velocity depends on the frame in which it is measured, so must the value of mass, so that the product of mass and velocity has the same value in any frame. In fact the mass of a moving object is found to be greater than the mass of the same object when measured at rest.

E=mc^2

This is probably the most famous formula in physics but do you know what it means?

Lets have a small review on work and energy. We know that if we apply force to an object of certain mass, the velocity of that object will increase [don't consider pushing against the wall, it won't move. But just think of a light object, like a stationary book. If you give it a push, its velocity will increase.]. Since force acts on an object over a distance, work is done on the object whose energy also increases (we know that energy is the ability to do work. Consider when you lift an object to a certain height. Its potential energy increases.). So if we apply greater force ,its velocity will increase greatly. But how much can you increase the velocity? We all know that speed of light is the ultimate speed limit in this universe. So what happens when we push an object so hard that its velocity increases to "c". Since its velocity cannot increase, its mass increases considerably. Note that the mass approaches infinity as the speed approaches the speed of light. Thus, it would take infinite energy to accelerate a massive object to the speed of light; another way of saying this is no massive object can ever travel at the speed of light relative to us.

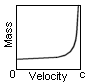
The graph below gives us an idea what happens to the mass of an object when its velocity approaches "c".

So we can say that work done on an object is used to increase its mass while normally, work is done to increase its energy. This leaves us with the result that mass and energy are equivalent.

Hence Einstein deduced the equation: E = mc^2

In this equation , E is the energy of an object

M is it's relativistic mass (this is calculated by the mass increase formula).

C is the speed of light

This theory can be seen into effect in an atomic bomb explosion where a small mass is converted into large amounts of energy. [large enough to supply a city with electricity for several years.]

Did you understand it now? You think you can make a BIG ATOMIC BOMB out of an apple?

But there is one thing that that you should know that conversion of mass into energy occurs only in specific situations. And the mass don't have to travel at the speed of light of light to obtain energy. C^2 acts like a constant that allows us to determine the energy released if a mass is transformed into energy.

================================================================

Now that we have everything in order let’s have a go at solving the equation. We will use a mass of 1kg to keep things simple and I will list all of the workings of the equation. So, with 1kg of mass (around 2.2 pounds) we get:

So from 1kg of matter, any matter, we can get out 9 ´ 1016 joules of energy

That is a lot of energy! For example, if we converted 1 kg of mass into energy and used it all to power a 100 watt light bulb how long could we keep it lit for? The first thing to do is divide the result by watts (remember that 1 watt is 1 joule per second):

That will be equal to 28,519,279 years !!